Bentuk dan Arti Simetri Lipat dan Simetri Putar

Bentuk dan Arti Simetri Lipat dan Simetri Putar

Dibawah ini adalah Bentuk dan Pengertian Simetri Lipat dan Simetri Putar:

Simetri Lipat dan Simetri Putar

Pengertian Simetri Lipat yaitu jumlah lipatan yang dapat dibentuk oleh suatu bidang datar menjadi 2 bagian yang sama besar. Untuk mencari simetri lipat dari suatu bangun datar maka dapat dilakukan dengan membuat percobaan dengan membuat potongan kertar yang ukurannya mirip dengan yang akan diuji coba. Lipat-lipat kertas tersebut untuk menjadi dua bagian sama besar. Jika suatu bangun dilipat menjadi dua, sehingga lipatan yang satu dapat menutup bagian yang lain dengan tepat, maka dikatakan bangun tersebut memiliki simetri lipat.

Pengertian Simetri Putar yaitu jumlah putaran yang dapat dilakukan terhadap suatu bangun datar di mana hasil putarannya akan membentuk pola yang sama sebelum diputar, namun bukan kembali ke posisi awal. Suatu bangun mempunyai simetri putar jika ada satu titik pusat dan bangun tersebut dapat diputar kurang dari satu putaran penuh sehingga bayangannya tepat pada bangun semula. Percobaan dapat dilakukan mirip dengan percobaan pada simetri lipat namun caranya adalah dengan memutar kertas yang telah dibentuk. Jika suatu bangun datar diputar melalui pusatnya dan dapat tepat menempati tempat semula maka dikatakan bangun tersebut memiliki simetri putar. Banyaknya bangun tersebut menempati tempat semula dalam sekali putaran menjukkan jumlah simetri putar. Arah perputaran mengikuti arah jarum jam.

RUMUS MATEMATIKA LENGKAP UNTUK ANAK SD
 
Sumbu simetri merupakan garis yang membagi suatu bangun menjadi dua bagian sama besar. Berikut ini sumbu simetri dari beberapa bangun datar

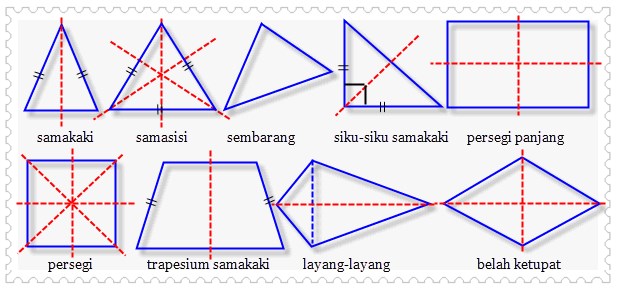
Simetri Lipat
Pengertian secara singkat simetri lipat pada bangun datar bisa didefinisikan sebagai banyaknya lipatan pada bangun datar yang bisa membagi bangun datar tersebut sehingga setengah bagian dari bangun datar tersebut bisa menutupi setengah bagian yang lain. Garis yang dapat membagi sebuah bangun datar menjadi dua dan kongruen disebut sebagai sumbu simetri. 

Perlu kalian ketahui bahwasannya tidak setiap bangun datar memiliki garis yang dinamakan sebagai sumbu simetri. Ada beberapa bangun datar yang tidak memiliki sumbu simetri sama sekali. Kalian bisa melihat beberapa bangun datar yang memiliki sumbu simetri pada gambar berikut.
 

Pada gambar di atas garis atau sumbu simetri digambarkan dengan garis putus-putus.  Apabila kita melipat atau memotong sebuah bangun datar dengan mengikuti garis-garis simetri tersebut maka bangun datar itu akan terbagi menjadi dua bagian yang sama besar.

Simetri Putar
Sebuah bangun datar dapat dikatakan memiliki simetri putar apabila ia memiliki sebuah titik pusat dan apabila bangun datar tersebut dapat kita putar kurang dari satu putaran penuh untuk mendapatkan bayangan yang tepat seperti bangun semula. Sebagai contoh coba kalian perhatikan gambar berikut ini:

Pada gambar di atas, ada sebuah bangun datar berbentuk segitiga sama sisi. Jika kita memutar segitiga tersebut sebanyak 1/3 putaran berlawanan ara jarum jam, maka bentuknya akan tetap sama seperti semula. Kemudian jika kita memutar segitiga sama sisi tersebut sebanyak 2/3 putaran hasil bayangannya tetap sama persis dengan bangun semula. Itu artinya segitiga sama sisi memiliki 3 simetri putar.

Apabila kita memutar sebuah bangun datar dan hanya bisa mendapatkan bayangan seperti bangun semula dalam 1 putaran penuh, artinya bangun datar tersebut tidak memiliki simetri putar sama sekali. Contohnya adalah trapesium, bangun datar ini tidak memiliki simetri putar karena kita harus memutar sebanyak 1 putaran penuh untuk memperoleh bentuk bayangan trapesium seperti bentuk bangun semula.

Tidak semua bangun datar memiliki simetri putar dan simetri lipat. Beberapa bangun datar ada yang hanya memiliki simetri putar, sementara yang lain ada yang hanya memiliki simetri lipat. Kalian bisa melihat daftar simetri lipat dan simetri putar yang dimiliki oleh tiap-tiap bangun datar pada tabel berikut ini:

 

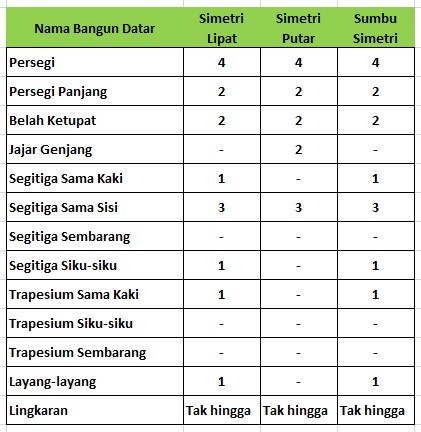
Demikianlah penjelasan sederhana yang bisa disampaikan oleh Blog tugas belajar anak SD. semoga bermanfaat.

sumber: Tugas Belajar anak SD